Home
Les phénomènes synchronistiques en tant que corrélations d’intrication dans la Théorie Quantique Généralisée

Les phénomènes synchronistiques en tant que corrélations d’intrication dans la Théorie Quantique Généralisée

Dans cet article, publié dans le Journal of Consciousness Studies en 2007, les auteurs, tous d’origine allemande, exposent quelques principes d’un modèle théorique général en parapsychologie. Ce modèle original associe théorie des systèmes et physique quantique, dans un rapprochement qui se distingue clairement des analogies hasardeuses entre phénomènes psi et phénomènes quantiques. Même s’il nécessite encore davantage de confirmation par de nouvelles données expérimentales, il rend déjà compte de la majorité des résultats obtenus par la parapsychologie expérimentale. Quelques exemples sont développés dans l’article, contrastant avec d’autres parties plus techniques.


Résumé : Les phénomènes synchronistiques ou psi sont interprétés comme des corrélations d’intrication dans une théorie quantique généralisée. En partant du principe que des corrélations d’intrication ne peuvent pas être employées pour une transmission d’information, nous pouvons déduire l’effet de déclin, fréquemment observé dans les expériences psi, et nous proposons des stratégies pour le supprimer et améliorer la visibilité des effets psi. Des exemples illustratifs sont discutés.

1. Introduction

Les phénomènes dits paranormaux tel que la télépathie, la psychokinèse ou la précognition sont notoirement mystérieux et de nature élusive. Bien que nullement rares, si l’on en croit la fréquence à laquelle ils sont rapportés (Greeley, 1987 ; 1991 ; Bauer & Schetsche, 2003 ; Moore, 2005), toutes les tentatives pour les appréhender rigoureusement et les produire d’une manière fiable échouent invariablement. Pour les sceptiques, c’est une raison suffisante de douter complètement de leur existence (Alcock, 2003).

La théorie de la synchronicité énoncée par C.G. Jung et W. Pauli (Atmanspacher et al., 1995) interprète les phénomènes paranormaux non comme le résultat d’une quelconque influence causale de l’esprit sur la matière ou sur d’autres esprits, mais comme des coïncidences significatives, c’est-à-dire des corrélations qui ne sont pas produites par une interaction causale telle que les physiciens la connaissent et l’appliquent avec succès, mais rendues possibles par des correspondances de sens et de signification. En fait, les phénomènes paranormaux se présentent typiquement comme d’apparentes coïncidences dérangeantes, inappropriées, peu probables, et souvent perçues comme porteuses d’un message pertinent voire essentiel pour les personnes impliquées. Ils se produisent habituellement dans des situations de tension émotionnelle élevée et de réceptivité au sens de tels messages.
En raison de l’échec mentionné ci-dessus concernant la production et la reproduction fiables des phénomènes paranormaux, plutôt que d’insister avec ténacité pour essayer d’identifier les mécanismes causaux permettant de les comprendre et de les produire, il semble plus avisé, selon nous, d’étudier l’approche synchronistique en l’intégrant dans un cadre de travail formel, afin de voir quelles compréhensions, prédictions et conclusions peuvent en être dégagées. C’est ce qui sera fait dans le présent article.
Les corrélations non-causales et non-locales telles qu’elles sont postulées dans la théorie de la synchronicité sont souvent rapprochées de ce qui est connu dans la théorie quantique sous le nom de « corrélations d’intrication ». Un système quantique composite en état intriqué montrera des corrélations entre les résultats des mesures d’observables concernant ses composants. Un exemple standard simple est un système de deux particules de spin 1/2 en singulet ou triplet montrant des corrélations d’intrication strictes entre les valeurs mesurées de la même composante de spin de chacune des deux particules. Une conséquence élémentaire de la théorie quantique est que ces corrélations d’intrication ne peuvent pas être employées pour transmettre une information ou pour exercer des influences contrôlables. (Cette conséquence vaut même dans le cas particulier où, par une certaine violation de la localité d’Einstein, les corrélations d’intrication sont produites par des causes physiques étranges. Pour une discussion plus détaillée, nous nous référons à l’annexe de cette étude.)
À partir de cette similitude entre les corrélations synchronistiques et les corrélations d’intrication dans les systèmes quantiques, il y a beaucoup de spéculations concernant le fait que les corrélations synchronistiques sont réellement un effet découlant de la théorie de la physique quantique. Nous préférons être prudents et éviter une supposition aussi forte pour au moins deux raisons. D’abord, elle semble présupposer un réductionnisme physique fort, qui affirme que des entités mentales, qui, après tout, sont impliquées dans des phénomènes synchronistiques, puissent être complètement décrites en termes physiques. Deuxièmement, les phénomènes physiques quantiques apparaissent habituellement dans les systèmes microscopiques, et les mécanismes d’amplification proposés pour les étendre aux systèmes macroscopiques et psychiques ont l’air plutôt artificiels.
Il est donc nécessaire de passer par un formalisme qui généralise la théorie de la physique quantique au-delà du cadre de la physique ordinaire, de telle manière que des concepts quantiques comme la complémentarité et l’intrication gardent une signification formelle définie. Un tel formalisme est en effet disponible sous le nom de Théorie Quantique Faible ou de Théorie Quantique Généralisée (Atmanspacher et al., 2002). La Théorie Quantique Généralisée prend en compte les notions de systèmes, d’états et d’observables de la théorie quantique ordinaire, mais les systèmes peuvent être d’un genre beaucoup plus général, par exemple, des groupes d’individus conscients. L’ensemble des états, à la différence de ce qu’il y a dans la théorie quantique ordinaire, n’est pas en général un espace de Hilbert, et les observables sont identifiées avec des procédures transformant des états en d’autres états, et peuvent être liés à n’importe quel aspect d’un système pouvant être étudié d’une manière significative. Comme dans la théorie quantique ordinaire, la complémentarité peut être attribuée au fait que les observables, en tant que fonctions, n’ont pas besoin de permuter entre elles, et l’intrication peut surgir dans des situations dans lesquelles les observables globales, appartenant à un système vu comme un tout, ne peuvent pas permuter avec certaines observables locales appartenant à des parties du système.
L’impossibilité de transmettre de l’information ou une action causale contrôlable au moyen de corrélations d’intrication, facilement prouvable dans la théorie quantique ordinaire, est élevée au statut d’axiome dans la Théorie Quantique Généralisée. Ceci produit une implémentation formelle bien définie de l’idée principale de la théorie de la synchronicité, et permet de la placer dans un contexte plus large. Nous démontrerons comment cet axiome aux effets apparemment négatifs peut être transformé en prédictions positives concernant la nature des phénomènes psi, qui sont bien confirmées dans les tentatives de recherche systématique sur le paranormal. (De même, en physique, la deuxième loi de la thermodynamique, avec ses conséquences innombrables, peut être dérivée du fait négatif de l’impossibilité d’un mouvement perpétuel de deuxième ordre.)
Quelques unes des conséquences qui en dérivent sont :

 (a) L’effet bien connu de déclin : Toutes les fois qu’une expérience psi donne d’abord des résultats positifs, les données ou les réplications postérieures élimineront l’effet précédemment observé et, éventuellement après des renaissances trompeuses (voir la note 8), vont ensuite se stabiliser au niveau de l’hypothèse nulle.

 (b) La réciprocité entre la force de l’effet et la fiabilité des phénomènes psi : Plus un effet est important, moins il s’avère être reproductible, et vice versa.

 (c) L’élusivité (dérobade) : Quand on essaye d’isoler les phénomènes psi, ils ont tendance à disparaître de l’endroit où ils sont cherchés pour faire surface à un autre endroit où on ne les attend pas. C’est ce qu’on appelle l’effet de déplacement.

Basé sur notre modèle d’intrication des phénomènes synchronistiques, nous proposons des stratégies pour augmenter la visibilité des effets psi en réduisant l’influence détériorante de l’effet de déclin et en exploitant l’élusivité.
Le contenu de cet article est organisé de la façon suivante :
Dans la section 2, nous décrivons brièvement la Théorie Quantique Généralisée afin de rendre notre présentation raisonnablement étayée et pour constituer une base pour comprendre les arguments qui vont suivre.
Dans la section 3, nous montrons comment s’applique la Théorie Quantique Généralisée aux phénomènes synchronistiques.
Dans la section 4, nous décrivons des stratégies pour planifier les expériences psi et, dans la section 5, nous donnons quelques exemples illustratifs. La section 6 récapitule nos conclusions. Nous avons enfin ajouté une annexe à l’attention du lecteur, dans laquelle nous montrons comment l’impossibilité de transmission de signal à partir du phénomène de corrélation d’intrication découle du formalisme de la théorie quantique et nous discutons de la signification de ce résultat.

2. Un aperçu de la Théorie Quantique Généralisée

La Théorie Quantique Généralisée est une généralisation de la théorie quantique conçue pour s’appliquer au-delà de la gamme des systèmes physiques ordinaires. Elle a été obtenue en partant de la formulation algébrique de la théorie quantique et en laissant de côté tous les axiomes qui semblent être spécifiques au monde physique. La structure restante est plus générale, bien qu’encore suffisamment riche pour pouvoir toujours décrire des phénomènes assimilés à la physique quantique comme la complémentarité (Walach & Römer, 2000) et l’intrication d’une manière bien plus générale. Ici, nous donnons un aperçu succinct de la structure de la théorie quantique généralisée. Pour des détails aussi bien que pour prendre connaissance de plusieurs applications de la Théorie Quantique Généralisée, nous vous référons aux publications originales (Atmanspacher et al., 2002 ; Atmanspacher et al., 2004 ; Römer, 2004 ; 2006 ; Walach & Schmidt, 2005).

Dans la Théorie Quantique Généralisée, les notions fondamentales de système, d’état et d’observable sont issues de la théorie de quantique ordinaire :

  • Un système Σ est une partie quelconque de la réalité dans le sens le plus général, qui peut, au moins en principe, être isolée du reste du monde et être l’objet d’une investigation.
  • On suppose qu’un système a la capacité de se trouver dans différents états. La notion d’état a également un côté épistémique, reflétant le degré de connaissance qu’un observateur a au sujet du système. À la différence de la mécanique quantique ordinaire, on ne suppose pas que l’ensemble Z des états a une structure sous-jacente d’espace de Hilbert.
  • Une observable A d’un système Σ est n’importe quel trait de Σ qui peut être étudié de la manière (plus ou moins) significative. Soit Lucadou_Romer_Walach_-_A.jpg l’ensemble des observables. Tout comme dans la mécanique quantique ordinaire, les observables A de Lucadou_Romer_Walach_-_A.jpg peuvent être identifiées avec des fonctions sur l’ensemble des états : Chaque observable A Є Lucadou_Romer_Walach_-_A.jpg associe à chaque état z Є Z un autre état A (z) Є Z. Comme fonctions sur l’ensemble des états, les observables A et B peuvent être composées en appliquant A après B. La combinaison AB définie comme AB (z) = A (B(z)) est également considérée comme une observable. Les observables A et B sont dites compatibles ou commensurables si elles permutent, c’est-à-dire, si AB = BA.
    Des observables qui ne permutent pas avec AB ≠ BA sont appelées complémentaires ou incompatibles. Dans la théorie quantique ordinaire, les observables peuvent aussi être ajoutées, multipliées par des nombres complexes et être conjuguées, et l’ensemble des observables est doté d’une structure riche appelée structure algébrique C*. Dans la Théorie Quantique Généralisée, les observables peuvent seulement être multipliées par la composition ci-dessus. Ceci donne à l’ensemble des observables une structure beaucoup plus simple appelée structure de semigroupe. Dans Atmanspacher et al. (2002), la Théorie Quantique Généralisée est caractérisée par une liste d’axiomes. Nous donnons ici seulement les propriétés les plus importantes :
  • Pour toute chose observable A Є Lucadou_Romer_Walach_-_A.jpg, il existe un ensemble associé specA qui est appelé son spectre. L’ensemble specA est juste l’ensemble des différents résultats possibles (ou ‘mesures’) correspondant à l’observable A.
  • Les propositions sont des observables spéciales P avec PP=P et specP Lucadou_Romer_Walach_-_C.jpg oui, non. Elles correspondent simplement à des questions oui-non à propos du système Σ. Pour chaque proposition P il existe une négation Lucadou_Romer_Walach_-_non-P.jpg compatible avec P. Pour les propositions compatibles P1 et P2, il existe une conjonction Lucadou_Romer_Walach_-_conjonction_P.jpg et une adjonction Lucadou_Romer_Walach_-_ajonction_P.jpg. On suppose que les lois des propositions logiques ordinaires restent valables pour les propositions compatibles.
  • Si z est un état et P une proposition, et si une mesure de P dans l’état z donne la réponse “oui” alors P(z) est un état pour lequel P est vrai avec certitude. Ceci met en valeur la nature constructive de la mesure pour la préparation et la vérification.
  • La propriété suivante généralise la propriété spectrale des observables dans la théorie quantique ordinaire. Pour chaque observable A et à chaque élément α Є specA, il existe une proposition Aα, qui est justement la proposition que α est le résultat d’une mesure de A. Alors,
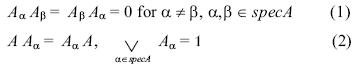
    Lucadou_Romer_Walach_-_Formule.jpg

    où 0 et 1 sont justement des propositions triviales qui sont jamais et toujours vraies, respectivement. De plus, une observable B permute avec A si et seulement si B permute avec tous les Aα.

Nous avons déjà mentionné que la Théorie Quantique Généralisée est assez riche pour englober les notions de complémentarité et d’intrication. Pour les observables complémentaires A et B avec AB ≠ BA, l’ordre de leurs mesures a de l’importance, et, de même que dans la mécanique quantique ordinaire, elles ne vont pas, en général, posséder d’états dans lesquels les deux à la fois ont une valeur bien définie avec certitude.
L’intrication peut surgir si des observables globales concernant tout le système Σ sont complémentaires à des observables locales concernant des parties de Σ. Si, en outre, le système est dans un état intriqué, par exemple dans un état dans lequel une observable globale a une valeur bien définie, il y a des corrélations d’intrication typique sans interaction entre les résultats des mesures des observables locales. Dans la théorie quantique ordinaire, il peut être prouvé que l’intrication ne peut pas être utilisée pour la transmission de signal ou l’intervention causale contrôlée : Si Σ1 et Σ2 sont différents sous-systèmes d’un système composite Σ, la distribution des valeurs des mesures effectuées sur Σ1 ne permet pas de dire si des mesures ont été effectuées sur Σ2, ou non, à moins que les résultats des mesures sur Σ2 soient connus sur Σ1. La preuve de ce fait est indiquée dans l’annexe. Ceci est indépendant de n’importe quelle hypothèse concernant la séparation des sous-systèmes dans l’espace et le temps. Si, cependant, on considère que la théorie de relativité restreinte est valide, comme de nombreuses preuves le suggèrent, et si la séparation des sous-systèmes est un intervalle de genre espace au sens de la théorie de relativité restreinte, alors la possibilité de n’importe quelle interaction physique causale peut être exclue comme mécanisme pouvant produire des corrélations intriquées. Dans la Théorie Quantique Généralisée, l’impossibilité du transfert de signal par des corrélations intriquées ne peut probablement pas être dérivée des autres axiomes, mais on s’attend fortement à ce qu’elle soit vraie et il peut être avisé de postuler de la considérer comme un axiome additionnel (Römer, 2003 ; 2004) :

  • Des corrélations d’intrication ne peuvent pas être employées pour transmettre des signaux ou des influences causales contrôlables.

En fait, la violation de cet axiome provoquerait un très sérieux danger de voir émerger des interventions paradoxales du genre « tuer son propre grand-père dans un passé lointain ».
Cet axiome sera employé fréquemment par la suite et ses conséquences seront étudiées dans le cadre formel de la Théorie Quantique Généralisée. Appelons-le l’axiome NT (“Non Transmission”).
Comme dans la théorie quantique ordinaire, le résultat d’une mesure n’est en général pas déterminé par l’état, mais remarquons que la Théorie Quantique Généralisée, au moins dans sa version minimale présentée ici, n’associe pas des probabilités quantifiées aux résultats d’un mesure d’une observable A. Ceci est lié à l’absence d’une structure d’état de Hilbert de l’ensemble Z des états. D’ailleurs, la notion de temps est complètement absente dans la formulation générale de la Théorie Quantique Généralisée.
La constante de Planck h qui commande le degré de non commutativité dans la théorie quantique ordinaire, n’entre pas dans la Théorie Quantique Généralisée. Par conséquent, des effets macroscopiques de complémentarité et d’intrication doivent être prévus dans des circonstances appropriées.
En mécanique quantique ordinaire, il est possible de dériver les inégalités de Bell et de conclure que l’indétermination de la théorie quantique n’est pas épistémique, c’est-à-dire due à une connaissance incomplète du ‘vrai’ état du système, mais ontique et profondément enracinée dans la notion même d’état quantique. Dans la Théorie Quantique Généralisée, il n’y a pas de base pour une telle déduction. Au contraire, la Théorie Quantique Généralisée sera fréquemment une description phénoménologique de systèmes complexes, avec couplage fort et contrôle limité, et les caractéristiques quantiques comme l’indétermination, la complémentarité et l’intrication résulteront de raisons épistémiques plutôt innocentes comme la connaissance incomplète, les interactions incontrôlables et, en particulier, les perturbations inévitables dues au processus de mesure. Dans cette situation il ne peut pas être exclu que des corrélations d’intrication puissent être produites par des interactions causales, mais elles ne peuvent toujours pas être employées d’aucune manière contrôlable pour transmettre de l’information ou des influences causales, et l’axiome de NT demeure vrai.
Cette remarque sera importante dans la section suivante.

3. La synchronicité et la Théorie Quantique Généralisée

Les phénomènes paranormaux ou synchronistiques se produisent dans les systèmes complexes de personnes et de parties du monde physique, qui sont fortement couplées par beaucoup de liens physiques, mentaux et en particulier émotionnels. Les systèmes de cette sorte ont une propriété, appelée la fermeture organisationnelle dans la théorie des systèmes. Varela a formulé la « Thèse de la Fermeture » de la façon suivante : « Chaque système autonome est organisationnellement clos ». Le système cellulaire ou le système immunitaire peut servir d’exemple en biologie et la conscience humaine peut être un exemple en psychologie. Il définit une unité organisationnellement close comme un réseau d’interactions qui régénèrent périodiquement le réseau comme une unité dans l’espace (pour des détails voyez : Varela, 1981). L’observation exercera des effets incontrôlables sur l’état de tels systèmes, et ceci en fait des objets privilégiés pour l’application de la Théorie Quantique Généralisée. Les systèmes organisationnellement clos sont composites et ont ainsi la capacité d’être dans des états intriqués. Comme mentionné auparavant dans l’introduction, nous allons porter une attention particulière aux corrélations intriquées entre les parties de tels systèmes fortement complexes et les associer aux phénomènes synchronistiques. La majeure partie de la recherche et de la discussion est centrée sur l’exclusion de n’importe quel mécanisme « normal » qui pourrait produire ces phénomènes. Dans notre terminologie, ceci amène à la question de savoir si les caractéristiques quantiques du système décrit par la Théorie Quantique Généralisée sont d’origine ontiques ou épistémiques. Dans des situations favorables, la possibilité d’interactions physiques causales entre les parties d’un système peut être éliminée, par exemple, si la séparation spatiale et les décalages temporels sont tels que ces signaux devraient être supralumineux[[Ce qu’on appelle les « expériences de pressentiment » peuvent servir d’exemples (Bierman & Radin, 1997).]]. Un autre cas présentant des opportunités est celui des phénomènes comme la précognition où l’ordre temporel entre la cause et l’effet est inversé et où l’existence de telles paires inversées d’événements pourrait produire des paradoxes d’intervention comme le fait de tuer son propre grand-père. Toutefois, en général, et également en particulier dans les cas les plus intéressants, il est extrêmement difficile sinon impossible de se décider sur cette question, et cela ne fait de différence ni pour notre description phénoménologique, ni pour notre analyse.
L’identification des systèmes organisationnellement clos auxquels notre formalisme devrait être appliqué est un problème non trivial, en particulier parce que les corrélations d’intrication entre des systèmes apparemment disjoints ne peuvent jamais être exclues avec certitude. Un des plus petits systèmes imaginables serait une simple personne, sur laquelle on pourrait observer des phénomènes psychosomatiques comme la somatisation. Mais, normalement, de tels phénomènes ne sont pas considérés comme paranormaux ou synchronistiques et, dans la Théorie Quantique Généralisée, ils devraient plutôt être considérés comme un effet de la complémentarité de l’esprit et du corps sur les individus. Cependant, il semble qu’il y a là une transition qui pourrait glisser vers les phénomènes de ‘poltergeist’, lesquels pourraient être interprétés comme une prolongation de la somatisation dans le monde extérieur, et comme exemple important des corrélations d’intrication.
Au niveau suivant de complexité viendraient des systèmes de complexité intermédiaire se composant de plusieurs personnes et objets physiques et montrant des phénomènes comme la télépathie, la psychokinèse ou la précognition. Le plus grand système imaginable serait l’unus mundus de C.G. Jung, c’est-à-dire la totalité du monde, neutre en ce qui concerne la distinction de l’esprit et de la matière. Il pourrait être possible de jeter une certaine lumière sur des phénomènes de l’histoire culturelle, l’apparition des modèles dans l’art, l’invention des concepts philosophiques ou scientifiques et leur rapport mutuel, mais également sur les mouvements de masse et l’hystérie en appliquant la Théorie Quantique Généralisée à l’unus mundus et en regardant les corrélations d’intrication.
Les phénomènes paranormaux sont habituellement associés avec le niveau intermédiaire de la complexité qui vient d’être mentionné.
Des phénomènes synchronistiques peuvent être attendus si un tel système est préparé dans un état d’intrication. Ceci peut en général être fait en se rendant sûrs que le système est dans un état propre z d’une observable globale A, c’est-à-dire dans un état dans lequel le système réside après qu’une mesure de A ait donné un certain résultat défini α Є specA. Par exemple, pour un système opérationnellement fermé de plusieurs personnes, A peut être une observable qui mesure le degré de leur ‘accord émotionnel’ ou à quel point ils sont fondamentalement connectés, par exemple, par des liens familiaux. Dans un état d’intrication, on observera des corrélations entre les valeurs mesurées des observables locales pour différentes parties du système. Comme cela a déjà été mentionné et formulé en tant qu’Axiome NT et en accord avec ce qui a été observé des phénomènes psi, ces corrélations ne peuvent pas être interprétées comme résultant d’aucunes interactions causales contrôlables ou de signaux entre les parties du système.
La signification précise des termes ‘signal’ ou ‘interaction causale contrôlable’ dans le sens où nous l’employons dans cette étude est défini par le fait de remplir les conditions suivantes :

  • Il y a des paires prédéfinies de quantités, une du côté émetteur Σ2, une du coté récepteur Σ1.
  • Il y a une corrélation stable entre les valeurs enregistrées des quantités.
  • Des manipulations contrôlables du côté de l’émetteur sont possibles, et leur effet peut être enregistré du côté du récepteur.
  • Des conclusions sur la nature des manipulations doivent être possibles.

Les corrélations synchronistiques d’intrication peuvent parfois sembler spectaculaires, mais dès lors que, du fait de certaines fluctuations épisodiques, il semblerait qu’elles sont dues à une interaction causale, cet effet apparent sera éliminé si on essaye de le confirmer en améliorant les statistiques par des tentatives de réplication. C’est l’effet bien connu de déclin, dont beaucoup d’expérimentateurs ont fait l’expérience. L’effet de déclin sera d’autant plus rapide que l’effet original était fort : la réciprocité de la taille d’effet et de sa reproductibilité est une autre prédiction de la Théorie Quantique Généralisée. On peut même, avec un certain degré de confiance, inverser cette proposition et conclure que si une influence d’une partie du système sur l’autre est observée de façon reproductible, ce n’est pas un effet psi mais le résultat d’un effet physique ordinaire. Un autre phénomène prévisible de la Théorie Quantique Généralisée se nomme ‘dérobade’ ou ‘élusivité’. Les corrélations, si on essaye de les interpréter comme des signaux et de les valider statistiquement, peuvent même changer de signe ou disparaître tout à fait, ou bien se montrer dans des observables différentes et/ou entre des parties du système différentes. On s’attend à ce que ce phénomène d’élusivité soit observé, en particulier si le nombre de corrélations observables est grand et si la préparation dans l’état d’intrication a une stabilité limitée.
Les événements dits synchronistiques sont de très bons exemples de situations se produisant dans des systèmes qui incluent un grand nombre de corrélations intriquées potentiellement significatives. L’exemple initial du rêve de scarabée du patient de C.G. Jung, avec un coléoptère qui s’est mis à voler à la fenêtre au moment où la patiente rapportait ce rêve, en est une bonne illustration. La corrélation synchronistique n’a rien à voir avec l’objet précis et sa localisation mais avec la sémantique (état) (ou `signification’) des objets. Le ‘Modèle de l’Information Pragmatique’ (MPI) fournit une description phénoménologique des processus sémantiques de telles situations synchronistiques. Elle propose une opérationnalisation[[Il a été avancé qu’il n’était absolument pas clair que le concept de Varela de « fermeture organisationnelle » ou que le concept de l’«information pragmatique » de Weizsäcker puissent être « opérationnalisés » d’une façon suffisamment rigoureuse. Il est vrai que, jusqu’à présent, n’était disponible aucun emploi standard et opérationnel de ces concepts, mais dans (Lucadou, 1986) des approches expérimentales sont décrites, qui peuvent être interprétées dans la lignée de ce travail et de la Théorie Quantique Généralisée, et être considérées comme des premiers pas dans cette direction.]] possible du terme ‘signification’ (information pragmatique) en présentant des observables complémentaires telles que la ‘nouveauté’ et la ‘confirmation’ (Weizsâcker, 1974 ; Lucadou, 1998). Il est évident que le MPI peut être considéré comme un cas particulier de la Théorie Quantique Généralisée. L’information Pragmatique n’est pas localisable en termes physiques et ne peut pas être `étiquetée’. Dans l’exemple de Jung, la signification du scarabée a pu correspondre à n’importe quel coléoptère ressemblant ou même au mot `coléoptère’ s’il avait été écrit sur un bout de papier qui aurait volé, par exemple, en travers de la porte etc. Selon Rössler (1992), les objets qui ne peuvent pas être étiquetés créent des propriétés non-classiques. Dans les expériences psi spontanées, le nombre d’états sémantiques possibles est ouvert, mais dans les expérimentations, il est fixé par le cadre expérimental. Si dans un cadre expérimental l »effet’ était fixé à un simple état localisé (par exemple un envol de coléoptère est prévu) n’importe quelle autre réalisation avec la même signification serait exclue. C’est la raison pour laquelle les évaluations post hoc dans les expériences parapsychologiques montrent souvent des corrélations post-hoc très fortement significatives, qui n’avaient pas été considérées à l’avance (voir les exemples ci-après). Dans les cas de ‘poltergeist’, de nouveaux phénomènes se produisent habituellement alors que l’on s’attend à des phénomènes précédemment observés (Lucadou & Zahradnik, 2004). De tels ‘effets de déplacement’ sont typiques en parapsychologie.

4. Planification des expérimentations du Psi

Dans les expérimentations du psi, on essaye d’observer des effets psi dans des conditions qui sont aussi contrôlables que possible, les conditions de laboratoire étant le cas idéal. Dès le début, on doit s’attendre seulement à des effets plutôt faibles dans de telles situations. Pour améliorer la visibilité des effets synchronistiques on devrait, selon la Théorie Quantique Généralisée, suivre les stratégies suivantes :

  • On devrait prendre soin que la fermeture organisationnelle du système et sa préparation dans un état d’intrication ne soient pas détruits par les observations.
  • On devrait concentrer sa recherche sur les corrélations remarquables entre les différentes parties du système plutôt que sur des influences causales (isolées).
  • Afin de réduire l’effet de déclin, on devrait faire une utilisation positive du phénomène d’élusivité. Ceci peut être fait par l’enregistrement simultané d’autant de corrélations différentes que possible. Les effets psi apparaîtront alors comme des patterns statistiquement peu probables, transitoires et changeant de façon inattendue dans la matrice de corrélation.

En somme, avec de telles mesures, il ne sera jamais possible de surmonter complètement l’effet de déclin et de convaincre tous les sceptiques. Mais au moins la visibilité des phénomènes synchronistiques pourra être améliorée considérablement.
Dans un cadre expérimental mono-causal conventionnel, la variable indépendante A pourrait toujours être employée dans une réplication stricte pour coder un signal qui apparaîtra dans la variable dépendante B, en commutant la variable indépendante A en on et off. Si on suppose de façon incorrecte qu’une corrélation entre A et B, qui a été trouvée dans des expériences précédentes, est de nature causale, la réplication doit échouer en raison de l’axiome NT, si le système étudié est régi par des corrélations intriquées. De plus, ceci donne un critère pour une limite supérieure de la taille d’effet E dans n’importe quelle étude de réplication : Si on suppose que la statistique courante qu’est le score Z est le critère permettant de déterminer si A est commuté en on ou off, simplement à partir d’une variable B dépendante, alors au moins un bit d’information est transféré. Dans le cas le plus simple, la formule valable est E < const / √n ,
si n est le nombre de réplications. Il n’y a que pour les réplications strictes que const est vraiment une constante qui dépend du cadre expérimental. Puisque beaucoup de détails diffèrent même avec des réplications strictes, la formule est simplement un principe de base. Suivant les indications de (Lucadou, 2000), la taille de const n’est pas nécessairement petite et des renaissances de l’effet sont possibles (voir la note 8). Puisque ce principe s’applique pour chaque essai d’une session expérimentale, la taille d’effet lors d’une expérience du psi devrait diminuer avec le nombre d’essais. Une méta-analyse récente de 357 expériences sur la PK (Steinkamp et al., 2002) corrobore cette prédiction. Le graphique en entonnoir (funnel-plot, fig. 1) montre, à l’évidence, le déclin de la taille d’effet en fonction du nombre d’épreuves. Les auteurs de la méta-analyse interprètent le résultat comme l’indication que l’effet PK n’existe pas et est simplement un artefact statistique dû à la sélection des publications, etc[[On peut remarquer que la méta–analyse dans (Bösch et al., 2006) a été critiquée intensivement, avec notamment d’autres méta-analyses arrivant à des conclusions différentes, et une réfutation dans la même revue qui l’a éditée. Toutefois, d’après la connaissance des auteurs, cette critique traite principalement de la question de la sélection des études pour la méta-analyse et ne porte pas sur le déclin évident de la taille d’effet en fonction de n.]].


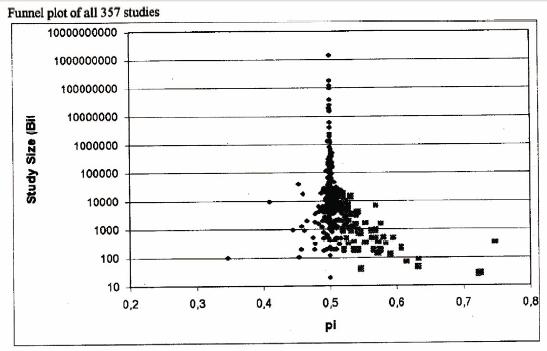
Lucadou_Romer_Walach_-_funnel_plot.jpg
Figure 1 : Graphique en entonnoir de 357 études de la PK (Steinkamp et al., 2002)

D’après ce résultat (voir section suivante), il ne semble pas utile de perpétuer la stratégie de recherches des expériences orientées vers la preuve, parce qu’une réplication stricte est la meilleure recette pour détruire l’effet.
Puisqu’on assume que l’axiome NT est responsable de ce fait, on pourrait résoudre le problème de deux manières :

  1. Le cadre expérimental est conçu de telle manière que seules les corrélations puissent être mesurées, et ne peuvent pas être (mal) employées pour tout transfert de signal, comme dans le cas EPR[[C’est naturellement le cas dans les expériences psi qui emploient des méthodes d’enregistrement neurophysiologique (Bierman & Radin, 1997 ; Wackermann et al., 2003), où le signal ne peut pas être extrait à partir du flux des données, parce que c’est seulement après avoir fait la moyenne de beaucoup d’épisodes d’EEG associés avec la stimulation que les corrélations peuvent être vues (voir ci-dessus). Indépendamment de ce fait, le système autorise beaucoup de degrés de liberté de par l’application d’électrodes multiples et en considérant à la fois les directions positive et négative de la corrélation (voir ci-dessous).]], et…
  2. Le dispositif expérimental permet à l’effet de se déplacer de façon imprévisible[[Une troisième possibilité serait de mélanger des variables non-locales à des variables causales d’une manière indistinguable. Dans ce cas, les signaux augmenteraient la fermeture organisationnelle du système et amplifieraient ainsi la corrélation non-causale dans le système psychophysique. Cependant, cette conception ne convaincrait jamais un sceptique, puisqu’on pourrait toujours argumenter que toutes les corrélations mesurées sont dues aux interactions causales et à aucun effet psi produit. On doit admettre que les expériences paranormales les plus spontanés souffrent de cette insuffisance méthodologique.]].

Il est difficile de réaliser la première condition dans une expérience psychophysique, parce que les variables psychologiques doivent être mesurées avant l’interaction psychophysique. Ces données pourraient toujours être employées pour faire des prédictions au sujet des variables physiques. Il n’importe pas que cette information soit réellement employée ou pas. Ceci constitue une différence importante par rapport aux situations EPR. Il n’y a que si l’interprétation des données psychologiques était générée post hoc (par exemple, par une nouvelle analyse factorielle des données) que ce problème pourrait être évité, mais cela est déjà très similaire à la méthode que nous allons présenter.

La deuxième condition peut être réalisée en employant de grands ensembles de variables psychologiques et physiques qui peuvent ou non se corréler dans le système psychophysique. Dans ce cas-ci, le résultat est une matrice de corrélation qui montre les corrélations psycho-physiques. La fermeture organisationnelle qui est créée par les conditions expérimentales (telles que l’instruction aux sujets, la clarté de ce qui est montré, la motivation des sujets etc.) permet l’interaction psychophysique qui apparaît dans le nombre et la force des corrélations dans la matrice. L’hypothèse nulle est donnée par le nombre de corrélations attribuables à la chance. Avec n’importe quelle réplication de l’expérience, la structure, la direction, et la force de ces corrélations peuvent changer, mais le nombre total et la force totale peuvent demeurer élevés si les conditions expérimentales restent semblables. Il est impossible de violer l’axiome NT parce qu’on ne connaît pas à l’avance quelles corrélations se révéleront et avec quel signe. Cette situation est comparable avec la situation EPR.
Comme il a été dit précédemment, la création de la fermeture organisationnelle du système psychophysique est d’importance primordiale. En outre, on doit faire attention à ce qu’elle soit créée principalement par des conditions expérimentales impliquant les sujets et non pas l’expérimentateur. Parfois les expérimentateurs sont plus motivés que les sujets, il est alors difficile d’interpréter les données et cela mène à ce qu’on appelle l’effet expérimentateur (Lucadou, 2000).

5. Exemples

L’exemple le plus impressionnant de l’effet de déclin après une réplication stricte est l’étude de réplication des expériences sur la PK de Princeton (PEAR) (Jahn, 1981 ; Jahn et al., 2000). Les auteurs écrivent :
Un consortium des groupes de recherche de Freiburg, Giessen et Princeton a été formé en 1996 pour poursuivre des études multidisciplinaires concernant les anomalies d’interaction machine / esprit. Le premier projet de collaboration entrepris a été un essai de réplication des expériences antérieures de Princeton qui avaient démontré des déviations anormales des données issues des Générateurs de Nombres Aléatoires électroniques, en corrélation avec des intentions émises par des opérateurs humains. Pour cette réplication, chacun des trois laboratoires participants a rassemblé les données de 250 * 3000 essais * 200 sessions expérimentales de données binaires, produites par 227 opérateurs humains. Un équipement identique de générateurs a été utilisé partout, des protocoles et procédures d’analyse fondamentalement semblables ont été suivis. Les données ont été divisées selon les trois types d’intentions de l’opérateur : pour augmenter la valeur moyenne des distributions de 200 échantillons binaires (HI), pour la diminuer (LO) ou pour ne pas l’influencer (BL). Des calibrages contigus effectués lors de l’absence d’opérateurs humains ont été pris en compte tout au long des expériences. L’agrément concernant le critère primaire convenu pour les effets anormaux était l’importance de la séparation des données HI-LO, mais des données ont également été rassemblées sur un certain nombre de corrélations secondaires. Le résultat primaire de cette réplication a été que, bien que les séparations moyennes globales HI-LO aient été dans la direction prévue pour chacun des trois laboratoires, les tailles globales de ces déviations ont échoué en ce qui concerne l’ordre de grandeur pour atteindre celui des expériences antérieures, ou pour atteindre le seuil significatif sur un plan statistique.

Si les résultats sont comparés à la première étude du groupe de Princeton, éditée en 1981, on peut observer un déclin fort de la taille d’effet.

Premier rapport PEAR (1981) Lucadou_Romer_Walach_-_Ehi-lo.jpg = 6000/13050 = 0.46
Ensemble des études PEAR
avant la réplication 		Lucadou_Romer_Walach_-_Ehi-lo.jpg = 35000/834000 = 0.042
Etude de réplication (2002) Lucadou_Romer_Walach_-_Ehi-lo.jpg = 7070/750000 = 0.0094

Tableau 1 : Taille d’effet des expériences PEAR et de ses réplications (les nombres proviennent des figures en références)[[Dans ce cas les données correspondaient tout à fait bien avec la formule donnée ci-dessus et const ≈ 50.]]

Dans le tableau 1, la taille d’effet est définie comme suit :
Lucadou_Romer_Walach_-_Ehi-lo_Thi_Tlo.jpg, T = Nombre d’essais réussis, n = nombre d’essais

Il est évident que la taille d’effet décline sans interruption avec chaque réplication[[Il a été objecté : « …que les auteurs ont apparemment lu (Jahn et al. 2000) sans remarquer que l’examen de la séquence chronologique des données des GNA du PEAR (fig. 12 et discussion associée) montre un premier effet fort, puis un déclin jusqu’à la performance nulle, suivie par une nouvelle augmentation jusqu’à obtenir encore des effets forts, ce qui est en parfaite contradiction avec le modèle des auteurs selon lequel il n’y aurait « aucun signal ». » Au contraire, c’est ce qui devait être attendu selon les prédictions du MPI et de la Théorie Quantique Généralisée. « Aucun signal » ne signifie pas qu’un effet dépassant significativement le hasard ne peut pas se produire, mais que les données doivent se comporter de telle manière qu’elles ne puissent pas être employées à la ‘reconstruction’ des conditions initiales (HI, LO, Ligne de base du hasard ou expectative théorique) uniquement à partir des données aléatoires. Si dans la deuxième étude (voir la figure 12 de Jahn et al., 2000), les données avaient été les mêmes que dans la première, une identification des trois conditions aurait été possible. Par conséquent, un retour à un effet nul devait être prévu par l’axiome NT. En conséquence, dans la troisième étude, un tel critère est absent. Et même un critère plus faible qui aurait été valable en combinant les deux premières études est éliminé par le fait que, dans la troisième étude, la condition de la ligne de base théorique ne peut pas être distinguée des conditions HI. D’après ces considérations, il est clair que la formule donnée ne tient que pour des situations très simples. Dans de vraies études, elle peut seulement être employée comme une règle générale qui marche toutefois étonnamment bien. Pour faire une prévision plus précise, il serait nécessaire de connaitre l’histoire de chaque expérience et le développement des critères des signaux pouvant être dérivés des données. Ceci inclut également les changements des conditions de mise en place durant l’expérience. D’après ce point de vue, seuls les résultats finaux des études sont employés dans le tableau ci-dessus.]]. Cependant, « l’effet psi » ne disparaît pas complètement, il se révèle dans d’autres variables au cours de l’évaluation post-hoc. Comme l’affirment les auteurs : « Diverses portions des données ont montré un nombre substantiel d’anomalies structurales internes dans des aspects tels qu’une réduction dans les écarts-type au niveau des essais ; des patterns irréguliers position de série ; et des dépendances différentielles sur différents paramètres secondaires, tels que le type de feedback ou la longueur de la session expérimentale, le tout se combinant bien au-delà des valeurs attendues selon le hasard. » Voir également Pallikari (2001) ; Atmanspacher et al. (1999).

Il faudrait mentionner ici qu’une prédiction clairement établie, fondée sur le MPI, décrivait l’orientation des résultats de la réplication avant qu’ils soient connus. Elle a été gardée jusqu’aux dernières minutes précédant l’évaluation finale, mais, malheureusement, on ne la mentionne pas dans le rapport final de recherches.
Le même cas de figure peut également être trouvé dans un autre domaine où les corrélations non-locales peuvent jouer un rôle crucial, à savoir l’homéopathie (Lucadou, 2002). Cependant, en homéopathie il n’y a pas une séparation aussi clairement définie entre les variables indépendantes (traitement homéopathique) et dépendantes (traitement du patient). Néanmoins un mécanisme causal semble peu probable car, du fait des dilutions élevées qui sont employées en homéopathie, presque aucune molécule de la substance curative n’est présente (Walach, 2003).
Bien qu’une série de tests cliniques ait été lancée récemment pour examiner l’homéopathie en employant le standard méthodologique conventionnel avec essais randomisés et contrôlant l’effet placebo, les résultats ne permettent pas de conclure. On voit très souvent un schéma similaire : Les paradigmes expérimentaux initiaux sont prometteurs et montrent de grandes déviations par rapport aux résultats dus au hasard, non compatibles avec l’hypothèse de la fluctuation aléatoire. Cependant, lors du test de réplicabilité, ces effets disparaissent. (Ce n’est pas le but de cet article de donner une vue d’ensemble de cette discussion, pour de plus amples détails, on consultera Walach (2003) ; Walach et al. (2005)).


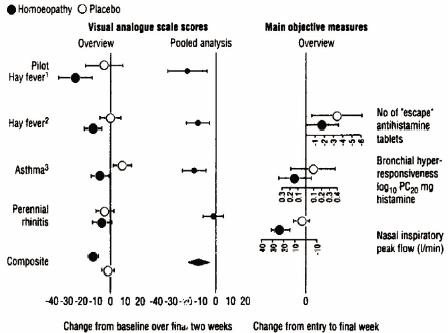
Lucadou_Romer_Walach_-_Taylor_homeopathy.jpg
Figure 2. Meta-analyse de quatre études sur l’homéopathie (Taylor et al., 2000).

Le problème principal de telles études semble ainsi être leur manque de répétabilité. Il pourrait y avoir beaucoup de raisons au manque de répétabilité comme des raisons psychologiques, ou des différences dans les variables environnementales, ou la régression vers la moyenne, et enfin et surtout l’axiome de non-transfert de signal (NT). Dans la plupart des méta-analyses il est difficile de trancher entre ces raisons. Cependant, dans la méta-analyse suivante (Taylor et al., 2000) des quatre études subséquentes sur l’homéopathie, les résultats peuvent être interprétés comme une conséquence de non-transfert de signal (NT).
Les résultats sont montrés sur la figure 2. La première colonne donne le nom de l’étude. La deuxième colonne montre la différence entre le groupe homéopathie et le groupe placebo mesurée par une échelle visuelle analogique. La troisième colonne montre la taille globale de l’effet et la quatrième colonne la différence du groupe homéopathie et du groupe placebo mesurée avec des méthodes différentes. La rangée ‘Composite’ donne l’effet composite des quatre études ensemble.
Deux genres de variables dépendantes avaient été employés pour mesurer l’effet thérapeutique : 1. L’échelle visuelle analogique subjective et 2. Différentes mesures objectives comme les concentrations en histamine et le pic de débit inspiratoire nasal. De notre point de vue théorique, il est important que, pour toutes les études, une variable (1.) ait été employée, la même pour toutes les études, avec, en plus, des variables non comparables (2.). Si l’hypothèse selon laquelle les corrélations non-locales jouent un rôle important est correcte, on pourrait prévoir le résultat suivant :

 (1) L’effet thérapeutique mesuré avec la même variable, comparable dans toutes les études (1.), diminuera pendant les études de réplication car la fiabilité statistique de cette variable est augmentée en raison du nombre croissant de cas (n) (effet de déclin).

 (2) L’effet thérapeutique mesuré avec des variables non comparables (2.) augmentera et ‘compensera’ le déclin de la taille d’effet de la variable comparable. Ainsi, la certitude pour prévoir de futurs résultats n’augmente pas avec n, pour des variables non comparables, parce que la direction et la force de l’effet restent inconnues (effet de déplacement).

Notez les tendances opposées dans la colonne 2 et la colonne 4. L’effet de déclin de la colonne 2 semble être compensé par l’augmentation de la différence mesurée avec une nouvelle variable de la colonne 4. En raison de l’homogénéité des études on peut supposer que la fermeture organisationnelle du système entier et, avec elle, son intrication non-locale restent constantes pendant les quatre études. Les résultats de la méta-analyse (figure 2) se montrent étonnamment en accord avec ces prévisions.
Finalement, on peut fournir un exemple dans lequel l’effet de déclin est au moins partiellement évité en contournant l’axiome de NT grâce à la technique de matrice de corrélations (voir ci-dessus). Dans ces expériences (Lucadou, 1986 ; 1991 ; 2006 ; Radin, 1993) (tableau 2) des variables psychologiques étaient corrélées avec des résultats dans des expériences de PK, avec feed-back et sans feedback (essais de contrôle). Seul le nombre des corrélations (significatives) entre les variables psychologiques et les variables physiques de l’expérience de PK sont comptées et comparées aux contrôles (Tests sans feed-back ou tests sans sujets).
Les variables psychologiques ont été mesurées avant les expériences de PK au moyen de questionnaires de personnalité standards. Il n’y a que dans les deux dernières études (Lucadou 2005a, b dans le tableau 2) que les variables psychologiques étaient des variables comportementales (appuyer sur des boutons, pour plus de détails voir (Lucadou, 2006)). Les variables physiques étaient plusieurs valeurs de test statistiques, qui décrivent des propriétés (telles que la valeur moyenne, la variance, l’auto-corrélation etc.) d’une séquence de variables aléatoires binaires (chaînes de Markov) produites par un générateur de nombres aléatoires quantique. Le générateur de nombres aléatoires physique a été soigneusement protégé contre toute influence physique des sujets.
Il s’est avéré que, dans toutes les études, la distribution globale des variables physiques n’a montré aucune déviation par rapport aux valeurs théoriques attendues, à la fois dans les conditions expérimentales et de contrôle. Plusieurs techniques ont été appliquées pour mettre en évidence un signal de PK (traceur) dans les séquences aléatoires expérimentales, mais aucun n’a été trouvé. C’est un argument fort pour supposer qu’en effet, aucun transfert de signal entre le sujet observant et le générateur de nombres aléatoires n’était impliqué. Néanmoins, le nombre de corrélations (significatives) entre les variables psychologiques et physiques a sensiblement augmenté pour les tests expérimentaux en comparaison du nombre de corrélations des tests de contrôle. La déviation est donnée dans le tableau 2 par les valeurs de Z.
Dans ces expériences, la taille d’effet (E = Z/√n, n = nombre de corrélations) dépend principalement de la fermeture organisationnelle du système. Ceci peut principalement être constaté dans les deux dernières expériences (Lucadou, a 2005, b) du tableau 2. . Les deux études ont eu une procédure identique et ont été effectuées en parallèle. Celle qui est à côté de la dernière dans le tableau (2005b), qui n’était pas significative, a été exécutée par des sujets non sélectionnés ayant une faible motivation (durant une conférence) tandis que toutes les études significatives (1986 ; 1991 ; 2005a) ont été exécutés par des sujets fortement motivés, qui sont venus au laboratoire parce qu’ils étaient intéressés à l’idée de participer à une expérience parapsychologique. Toutefois, une analyse plus détaillée montre que les sujets non sélectionnés (2005b) n’ont pas complètement échoué. Un sous-groupe (2005c) qui montrait le plus de ‘conduites innovantes’ a obtenu également une augmentation des corrélations. Enfin, on pourrait démontrer dans l’étude, que la structure de la matrice de corrélation n’est pas stable si l’expérience est répétée, mais que le nombre de corrélations demeure à peu près le même (pour plus de détails, voir Lucadou, 2006)[[Il avait été dit en critique que : « L’examen de plusieurs expériences par von Lucadou suggère que les auteurs ont une compréhension particulière du concept de « signal ». Bien qu’ils aient échoué à « trouver un signal de PK » dans les séquences aléatoires individuelles, les corrélations robustes et répétables rapportées dans le tableau 2 constituent en fait un signal ». Cet argument est uniquement vrai si, et seulement si, les différentes corrélations entre une variable donnée psychologique et une variable donnée physique restent stables si l’expérience est répétée. Mais ce n’est évidemment pas le cas, car seul le nombre de corrélations est conservé, mais pas la position précise des variables corrélées. Dans la section 3, on donne une explication du terme ‘signal’. Cependant, ce fait n’exclut pas la possibilité que certaines paires de variables psychologiques et physiques montrent des corrélations plus fortes, qui se produisent plus fréquemment avec des réplications. Ceci signifie que certaines régions dans la matrice de corrélations peuvent montrer une structure quelque peu prédominante indiquant certaines caractéristiques du système psychophysique en question, mais cela ne signifie pas qu’un signal est caché dans la matrice.]].
L’étude de D. Radin (1993) est la seule expérience indépendante dans la littérature qui a employé la technique de matrice de corrélations. Cependant, dans le cas de cette étude, il y avait seulement un sujet et les ‘variables psychologiques’ contenaient également des variables environnementales et par conséquent, l’étude n’est pas complètement comparable.

Etude N sigcorr N sujet Ps Var Ph Var # corr Z E
Luc1986[34] 75 299 24 23 552 5.13 0.218
Luc1991[35] 28 307 16 8 128 3.10 0.274
Rad1993[37] 32 1 16 23 368 2.63 0.137
Luc2005a[36] 39 386 27 18 216 6.22 0.423
Luc2005b[36] 11 386 27 18 216 0.04 0.003
Luc2005c[36] 21 220 27 18 216 2.25 0.153

Tableau 2 :
Résultats de l’ensemble des études (N sigcorr = nombre de corrélations significatives, N sujet = nombre de sujets, Ps Var = nombre de variables psychologiques, Ph Var= nombre de variables physiques, # corr = nombre de corrélations, Z= valeur de z, E = taille d’effet).

Les exemples, donnés ici, qui montrent le déclin et le déplacement, pourraient facilement s’ajouter à de nombreux autres, et ce serait un objet de recherche intéressant de mettre en application les idées présentées ici dans une future méta-analyse d’expériences comprenant des effets non-locaux.

6. Conclusion

Nous avons discuté le fait que les effets synchronistiques, anomalistiques ou psi sont probablement dus aux corrélations non-locales que l’on est en droit d’attendre, selon la Théorie Quantique Généralisée, dans des systèmes suffisamment clos, contenant des caractéristiques et des observables complémentaires locales et globales. Nous avons précisé qu’une telle interprétation se débarrasse de l’idée selon laquelle toutes les prétendues influences mentales directes sur les systèmes physiques sont des soi-disant signaux psi, car celle-ci créerait des difficultés théoriques violant différents théorèmes de l’invariance. Au contraire, cela permet une interprétation rationnelle des effets psi en tant que corrélations non-locales entre des éléments d’un système qui ne sont pas causaux et par conséquent non utilisables pour une transmission de signal. Le revers de ce fait est la difficulté qu’il y a à isoler expérimentalement de tels effets, puisque chaque tentative expérimentale pour isoler un effet équivaut en réalité à l’extraction d’un signal causal du bruit de fond. Cette approche explique deux caractéristiques dominantes des effets psi : l’élusivité et le déclin des résultats expérimentaux dans les réplications. Nous avons précisé qu’il existe néanmoins des stratégies indirectes, qui pourraient être employées pour la validation expérimentale de ce que nous avançons. Nous affirmons que c’est une explication rationnelle, en conformité avec les approches scientifiques traditionnelles, et espérons que cela prépare le terrain pour davantage de recherche créative, et son intégration éventuelle dans un cadre scientifique plus large.

7. Annexe : Le « théorème d’Eberhard »

Dans cette annexe, nous prouvons que l’impossibilité de transmettre l’information par des corrélations d’intrication, parfois désignée sous le nom du théorème d’Eberhard, est une conséquence directe du formalisme de la théorie quantique. De plus, nous discutons de la pertinence de ce résultat.

[Une partie de cette annexe étant très technique, nous avons préféré ne pas la traduire et présenter seulement l’originale. NdT]
Lucadou_Romer_Walach_-_Romer_part1.jpg
Lucadou_Romer_Walach_-_Romer_part2.jpg

Ainsi, aucun signal ne peut être transféré en choisissant et en mesurant une observable B sur l’autre partie du système. C’est la ‘propriété 4′ chez Eberhard (1978).
Les corrélations d’intrication pourraient seulement être employées pour la transmission de signal, si, sur un canal différent et pour chaque acte de la mesure, l’observateur à l’autre extrémité était informé de quelle observable a été mesurée et lesquelles de ses valeurs mesurées peuvent être gardées ou rejetées.
Le résultat concernant les distributions des valeurs mesurées est indépendant de la séparation spatiale ou temporelle des événements que constitue chaque mesure. Mais si la séparation de n’importe quelles paires de mesures des deux cotés du système composé du genre espace, et si la Théorie de la Relativité restreinte d’Einstein se tient (comme cela semble être le cas), alors les corrélations d’intrication ne peuvent être le résultat d’aucune interaction physique.
Sans la relativité restreinte, par exemple si on prétend que des interactions instantanées à distance sont possibles, on ne peut évidemment pas arriver à cette conclusion. Eberhard (1978) propose une violation de relativité restreinte par l’existence d’un système inertiel, dans lequel un événement E1 peut être la cause d’un événement E2 toutes les fois que E1 est avant E2. Dans un système différent, obtenu par une transformation de Lorentz, les deux événements ont pu être dans un ordre temporel inversé.
Même si par une certaine violation de la Relativité restreinte, les corrélations intriquées pouvaient être dues à des causes physiques, ceci n’infirme pas notre résultat général disant que, comme conséquence simple du formalisme de la Théorie Quantique, des corrélations intriquées ne peuvent pas être employées pour la transmission de signal sans l’aide d’un autre canal d’information.
L’impossibilité d’une transmission de signal au moyen de corrélations intriquées est une conséquence directe du formalisme de base de la théorie quantique. Peacock et Hepburn (1999) donnent une liste utile de références sur cette question, mais en raison des considérations présentées ci-dessus, il est très osé d’affirmer comme ils le font que les démonstrations de la propriété de non-signal sont petitio principii et qu’on ne peut pas exclure un transfert d’information et même d’énergie au moyen de corrélations d’intrication.
La seule manière de détruire la propriété « aucun signal » serait une modification des fondements mêmes de la théorie quantique, par exemple en décrivant les observables concernant les sous-systèmes non plus par des observables du type Lucadou_Romer_Walach_-_A_x_1.jpg mais par un autre opérateur. Mais il semble être impossible de le faire sans contredire des faits expérimentaux innombrables et bien établis, par exemple de la physique des atomes accompagnés de plusieurs électrons. D’ailleurs, avec la violation de la localité d’Einstein qui s’ensuivrait, des interventions paradoxales roderaient dans les parages.
D’une manière générale, la réduction d’état dans la théorique quantique ne mène pas à une contradiction entre la localité d’Einstein et la théorie quantique des champs. Des affirmations inverses faites par Hegerfeld ont été réfutées d’une manière convaincante et couramment acceptée par Buchholz et Yngvason (1994).

Références

Alcock, J.E. (2003), ‘Give the null hypothesis a chance: Reasons to remain doubtful about the existence of PSI’, Journal of Consciousness Studies, 10 (6-7), pp. 29-50.
Atmanspacher, H., Bösch, H., Boller, E., Nelson, R. D., Scheingraber, H. (1999), `Deviations from physical randomness due to human agent intention?’ Chaos, Solitons and Fractals, 10, pp. 935-52.
Atmanspacher, H., Filk, Th., Römer, H. (2004), ‘Quantum Zeno features of bistable perception, Biological Cybernetics, 90, pp. 33-40, http://arxiv.org/abs/ physics/0302005.
Atmanspacher, H., Primas, H., Wertenschlag-Birkhäuser, E. (ed. 1995), Der Pauli-Jung Dialog und seine Bedeutung für die moderne Wissenschaft (New York: Springer).
Atmanspacher, H., Römer, H., Walach, H. (2002), `Weak quantum theory: Complementarity and entanglement in physics and beyond’, http://arxiv.org/ ab s/quant-ph/0 104109, Foundations of Physics, 32, pp. 379-406. http://arxiv.org/abs/quant-ph/0 104109.
Bauer E., Schetsche, M. (ed. 2003), Alltägliche Wunder: Erfahrungen mit dem Übersinnlichen – wissenschaftliche Befunde (Würzburg: Ergon).
Bierman, D.J., Radin, D.I. (1997), Anomalous anticipatory response on randomized future conditions, Perceptual and Motor Skills, 84, pp. 689-90.
Bösch, H., Steinkamp, F., Boller, E. (2006), `Examining psychokinesis: The interaction of human intention with random number generators: A meta-analysis’,
Psychological Bulletin, 132 (4), pp. 497-523.
Buchholz, D., Yngvason, J. (1994),’There are no causality problems for Fermi’s two-atom system’, Physical Review Letters, 73, pp. 613-16.
Burns, J.E. (2003), ‘What is beyond the edge of the known world?’, Journal of Consciousness Studies, 10 (6-7), pp. 7-28.
Eberhard, P. (1978), ‘Bell’s theorem and the différent concepts of locality’, Nuovo Cimento, 46B, pp. 392-419.
Greeley, A. (1987), `Mysticism goes mainstream’, American Health, Jan/Feb, pp. 47-9.
Greeley, A. (1991), ‘The paranormal is normal: A sociologist looks at parapsychology’, The Journal of the American Society for Psychical Research, 85, pp. 367-74.
Jahn, R.G. (1981), ‘The persistent paradox of psychic phenomena: An engineering perspective. Proceedings of the IEEE 70 (2), pp. 136-70.
Jahn, R., Dunne, B., Bradish, C., Dobyns, Y., Lettieri, A., Nelson, R., Mischo, J., Boller, E., Bösch, H., Vaitl, D., Houtkooper, J., Walter, B. (2000),
`Mind/machine interaction consortium: PortREG réplication experiments’,
Journal of Scientific Exploration, 14 (4), pp. 499-555.
Lucadou, W. v. (1986), Experimentelle Untersuchungen zur Beeinflussbarkeit von stochastischen quantenphysikalischen Systemen durch den Beobachter (H.-A. Herchen Verlag: Frankfurt).
Lucadou, W. v. (1991), ‘Locating Psi-bursts: Correlations between psychological characteristics of observers and observed quantum physical fluctuations’, in The Parapsychological Association 34th Annunal Convention, Proceedings of Presented Papers, ed. D.L. Delanoy (Heidelberg: Parapsychological Association.), pp. 265-81.
Lucadou, W. v. (1998), ‘The exo-endo-perspective of non-locality in psychophysical systems, International Journal of Computing Anticipatory Systems, 2, pp. 169-85.
Lucadou, W. v. (2000), ‘Backward causation and the Hausdorff-Dimension of singular events’, in Proceedings of Presented Papers, ed. F. Steinkamp (Freiburg i.Br.: The Parapsychological Association 43rd Annual Convention August 17-20, 2000), pp. 138-47.
Lucadou, W. v. (2000), ‘Hans in luck: The currency of evidence in parapsychology’, The Journal of Parapsychology, 64, pp. 181-94.
Lucadou, W. v. (2002), ‘Homeopathy and the action of meaning: The model of pragmatic information (MPI) and homeopathy’, in Proceedings: Future Directions and Current Issues of Research in Homeopathy, ed. Harald Walach, Rainer Schneider, Ronald A. Chez (Freiburg).
Lucadou, W. v. (2006), `Self-organization of temporal structures: A possible solution for the intervention problem’, in: Frontiers of Time. Retrocausation: Experiment and Theory, ed. Daniel P. Sheehan, AIP Conference Proceeedings, Volume 863, AIP, Melville, New York, 2006, pp. 293-315.
Lucadou, W. v., Zahradnik, F. (2004), `Predictions of the model of pragmatic information about RSPK’, in Proceedings of Presented Papers, The Parapsychological Association 47rd Annual Convention August 5-8, 2004,ed. S. Schmidt (Vienna University). pp. 99-112.
Moore, D.W. (2005), ‘Three in four americans believe in paranormal: Little change from similar results in 2001’, Gallup News Service June 16.
Pallikari, F. (2001), ‘A study of the fractal character in electronic noise process’, Chaos, Solitons and Fractals, 12, pp. 1499-1507.
Peacock, K.A., Hepburn, B.S. (1999), ‘Begging the signalling question: Quantum signalling and the dynamics of multiparticle systems’, Proceedings of the 1999 Conférence of the Society for Exact Philosophy Report-no: UL- 1999- 1. http://arxiv.org/abs/quant-ph/9906036.
Radin, D. I. (1993), ‘Enviromental modulation and statistical equilibrium in mindmatter interaction’, Subtle Energies and Energy Medicine, 4, 1, pp. 1-29.
Römer, H. (2003), Neue Aspekte einer verallgemeinerten Quantentheorie, Talk Offenburg Oct. 2003, unpublîshed.
Römer H. (2004), `Weak quantum theory and the emergence of time’, Mind and Matter 2, pp. 105-25, quant-ph/0402011.
Römer, H. (2006), Substanz, Veränderung und Komplementarität, Phil. Jahrbuch 113, pp. 11 8-136.
Römer, H. (2006), Complementarity of Process and Substance, Mind and Matter 4, pp. 69-89.
Rössler, O.E. (1992), Endophysik: Die Welt des inneren Beobachters (Berlin: Merve Verlag).
Steinkamp, F., Boller, E., Bösch, H., (2002), ‘Experiments examining the possibility of human intention interacting with random number generators: A preliminary meta-analyses’, in The Parapsychological Association 45th Annual Convertion, Proceeding of presented Papers., ed. Caroline Watt (Paris), pp. 256-72.
Taylor, M.A., Reilly, D., Llewellyn-Jones, R.H., McSharry, C., Atchison, T.C. (2000), ‘Randomized controlled trial of homoepathy versus placebo in perennial allergic rhinitis with overview of four trial séries’, British Medical Journal, 321, pp. 471-6.
Varela, F. J. (1981), ‘Autonomy and autopoiesis’, in Self-organizing Systems, ed. G. Roth, H. Schwengler (Frankfurt: Campus), pp. 14-23.
Wackermann, J., Seiter, C., Keibel, H., Walach, H. (2003), ‘Correlations between brain electrical activities of two spatially separated human subjects’, Neuroscience Letters, 336, pp. 60-4.
Walach, H. (2003), ‘Entanglement model of homeopathy as an example of generalized entanglement predicted by weak quantum theory’, Forschende
Komplementärmedizin und Klassische Naturheilkunde, 10, pp. 192-200.
Walach, H., Jonas, W. B., Ives, J., van Wijk, R., Weingärtner, O. (2005), ‘Research
on homeopathy: State of the art’, Journal of Alternative and Complementary
Medicine, 11, pp. 813-29.
Walach, H., Römer, H. (2000), ‘Complementarity is a useful concept for consciousness studies. A reminder’, Neuroendocrinology Letters, 21, pp. 221-32.
Walach, H., Schmidt, S. (2005), ‘Repairing Plato’s life boat with Ockham’s razor:
The important fonction of research in anomalies for mainstream science’, Journal of Consciousness Studies, 12 (2), pp. 52-70.
Weizsäcker, E. v. (1974), Erstmaligkeit und Bestätigung als Komponenten der pragmatischen Information. In: E. v. Weizsäcker (Hrg.): Offene Systeme I (Stuttgart: Klett), pp. 83-113.

Correspondance :
Walter von Lucadou, WGFP, Hildastr. 64, 79102 Freiburg, Germany
lucadou@freenet.de
Hartmann Römer, Physikalisches Institut, University of Freiburg, Hermann-Herder-Str. 3, 79104 Freiburg,Germany.
hartmann.roemer@physik.uni-freiburg.de
Harald Walach, University of Northampton, School of Social Sciences, Samueli Instituts of Information Biology, European Office, Park Campus, Boughton Green Road, Northampton NN2 7AL, UK.
haraid.walach@northempton.ac.uk